
The first maps only showed local or regional areas using a grid technique with no distortion. When it became generally agreed that the earth wasn’t flat but a globe, a system was needed to convert 3D to 2D to show the entire known surface. From around the 2nd Century BC to the 16th Century AD the stereographic projection was used. The complex math required originated from the East. Commonly called a Planisphere, as the name implies, it involved projecting a plane onto a sphere.
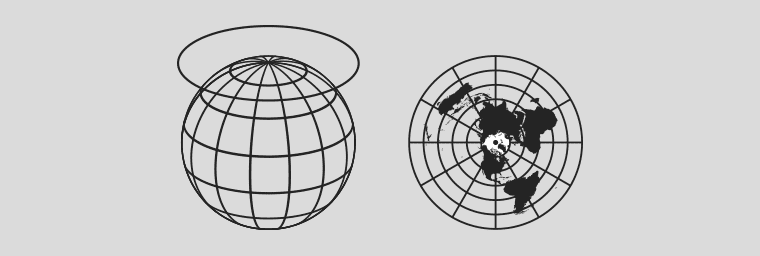
The great attraction of the projection is that the Earth appears as if viewed from space. It is a conformal projection in that shapes are well preserved over the map, although extreme distortions do occur towards the edge of the map. An interesting feature is that any straight line which has the centre of the earth as their centre is a ‘Great Circle’. The advantage being true distances can be calculated and the shortest distance between those points is always along a Great Circle.
Another is that when polar azimuthal, It sends meridians to rays emanating from the origin and parallels to circles centred at the origin. In short, this brought about the inception of Latitude, Longitude, Equator and Time Zones. Note the similarity with a clock face!
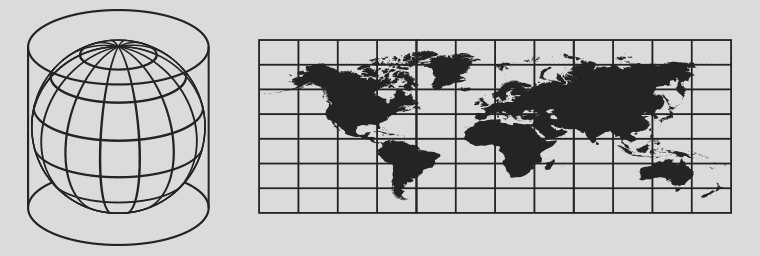
The globe concept brought about the need for dual hemispheres. The top down view of the stereographic projection wasn’t ideal for this. Hence the increasing number of dual planisphere maps up to the 16th Century. Then came Mercator’s 1569 map which, for the first time, displayed the now famous and widely used Mercator projection. Basically, he took the opposite approach and the cylindrical projection was born.
The latin title of his map can be translated into ‘A Nautical Chart of the World’. This meant a huge step forward for the safe and precise charting of a route at sea and quickly became the standard. It had the ability to represent lines of constant true direction (the same direction that a compass would show). In an era of sailing ships and navigation based on direction only, this was a vitally important feature of this projection. Considered generally a conformal projection, it displays extreme distortion regarding shapes away from the Equator. It has been relentlessly pushed to this day due to political reasons by the ruling nations geographical locations in the Northern Hemisphere.
It stands out due to the torrent of cylindrical and conic projections created around this time. A few other notable stereographs can be found such as Jacques Cassini’s 1721 rendition and Adolf Henze’s 1891 24 globe gores.
Alexander Gleason’s map is based on a north-polar azimuthal equidistant stereographic projection. Apart from being visually striking, it is extremely accurate and displays a wealth of information on time and distance. His map had the unique ability to display any time and time difference between two points internationally. Gleason received U.S. patent 497,917 for his map on May 23, 1893. Only 4 examples are known to exist.
